1.
There is a form of Buddhism so potent, adherents say, that to hear its name spoken is to receive a promise of premature enlightenment, of early freedom from the wheel of incarnations. Something similar is true of Srinivasa Ramanujan, the super-genius who was born into deep poverty in an obscure part of southern India, who taught himself mathematics from a standard textbook, and in total isolation became a mathematician of such power that a hundred years after his death, at the age of thirty-two, the meaning of much of his work is still a mystery. In the middle of what I thought would be my life’s work, writing and producing music, I heard his story; now I find myself in graduate school studying number theory.
The story of Ramanujan is a variation on the same mythopoeic tale related in Star Wars and the New Testament, of a special boy born into adversity. A mother cannot conceive. The Goddess appears in a dream, promising a son through whom the God will speak to his creation. While pregnant, the mother travels to her ancestral home. During the winter solstice, the boy is born, under signs in the heavens that portend great events: his horoscope, cast by his mother, predicts that he will be a genius beset by great suffering. “Svasti Sri,” it reads, “when the moon was near the star Uttirattadi, when Mithuna was in the ascendant, on this auspicious day” Ramanujan is born. And indeed, his will be a short life, full of triumph and disaster. Growing up, he is gentle and quiet. Weightless is the word one of his childhood acquaintances uses in Robert Kanigel’s The Man Who Knew Infinity: A Life of the Genius Ramanujan. Beginning in his teenage years, Kanigel writes, Ramanujan “would abruptly vanish… Little subsequently became known” about these disappearances. Around this time, Ramanujan acquires a hoary old text (G. S. Carr’s Synopsis of Elementary Results in Pure Mathematics) that initiates him into the arcana. The Goddess begins to appear to Ramanujan in his dreams, showing him scrolls covered in strange formulae. “Nākkil ezhutināl,” he later said. “She wrote on my tongue.”
With such minimal training, Ramanujan rediscovers the mathematics of the preceding millennia. As he begins to make deep discoveries of his own, he writes to the learned men of the world, but his claims seem too extraordinary to be the product of a sane mind, so they ignore him. One of these letters happens to reach G. H. Hardy, a famous number theorist at Cambridge University and one of the only mathematicians in the world with the right mix of training and temperament to see Ramanujan clearly. Confronted with Ramanujan’s mathematical locutions, such as this one, which uses an infinite “continued fraction” to relate e, π, and the golden ratio1 to one another,
Hardy realizes that Ramanujan’s formulae, so weird yet elegant, supercharged with meaning yet concise, “must be true because, if they were not true, no one would have the imagination to invent them.” So disturbed is Hardy by the genius evident in Ramanujan’s letter that he sends an emissary to the edge of the empire, to India, to bring Ramanujan back to the imperial capital.
At Cambridge, Ramanujan is friendly and funny, easy company, but weird mathematics gushes out of him. He can’t explain the reasoning that leads to his formulae, nor their significance. He seems otherworldly to Hardy, as easy and dexterous with infinite quantities as with a knife and fork. With his intellect finally being fed by a university, Ramanujan’s genius erupts into something never before seen. And then he begins to die. Tuberculosis is suspected and so, in line with the treatment of the day, his doctors force him to live in an open room fully exposed to the English winter. The food the doctors bring him, Ramanujan writes, is inedible: botched curries “as hard as uncooked rice.” His body wastes away until he is little more than a walking skeleton. Then he returns to India, expecting to die. As his last act, he produces the strangest work of his career: a series of mathematical formulae only recently understood. We now know that they grant the bearer passage to the infinite.
If I had heard any of this when I was growing up, in Ruston, Louisiana, in the 1980s, I might not have become a musician at all. As it happened, I instead heard the story of Brian Wilson, another special boy who burned up his mind searching for the infinite. My friends and I who started the Elephant 6 music collective wanted to be like Wilson and our other psychedelic idols, and to see through their eyes. What would the genius do? I’d ask myself, and then study old studio photographs to see what they had actually done. I taught myself to record by trying to re-create my idols’ sessions. Imagining myself in conversation with them gave me material. What was the idol trying to tell me?
One night, my band, the Apples in Stereo, were hours into a recording session when the tape machine’s motor exploded with a bang. The rest of the Apples went home. Alone in my studio’s control room, I ripped out all the burned-up diodes and cleared a space on the floor. I opened an electronics manual and, for the first time, read Ohm’s Law, V = I × R, the fundamental equation of electronics, which weaves together the three basic properties of an electrical circuit: voltage (V), current flow (I), and resistance (R). The text presented Ohm’s Law as a tool, a measuring device I could use to figure out what was happening inside the tape machine: a string of symbols in service to physical reality.
But this seemed backward. What was in service to what? If the formula was a tool for measuring the physical world, that implied that the physical world was the deeper reality, of which the equation provided only an approximation. If that was the case—if mathematics was subservient to reality—the equation would have failed, not the machine. I would have been sitting on the floor searching for a better formula, not installing fresh diodes. What in fact had happened was that the moment the physical world contradicted the equation, the diodes burned up and the electrons stopped flowing. The physical world gave way and the equation persisted. The equation, not the machine, was the fundamental entity. The machine was only a shadow.
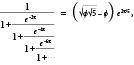
Basically, I got my mind blown by a broken tape machine. The challenge of the psychedelic experience, as the Beatles pointed out, comes after it is over. You have to find meaning in it, otherwise it was just an indulgence of the id. So, once again following my idols, I looked for the meaning. And it was this: electric guitars, stereophonic sound, magnetic tape, analog synthesizers, and the supreme joy of my life, making music with my friends, all existed because of a simple equation. What flowed through the circuits of the tape machine, through our headphones and our brains, what made us feel loved and allowed us to express our love wasn’t music, or even electricity, but numbers. Music, Brian Wilson said, was the voice of God; His language, said Galileo, was mathematics.
While on tour with the Apples, I started exploring mathematics, experimenting with formulae in dressing rooms and reading classic works by Euler, Einstein, and Riemann in the tour van. Then I heard the story of Ramanujan. Within a few years, I had upended my life, put the band on hold, and moved my family to Georgia to study with Ken Ono, a Ramanujan expert at Emory University.
A couple of years ago, with Ramanujan’s 125th birthday approaching, Ken decided to prove “something special”—he’s the kind of person who can just make a decision like that—so he took on the final mystery in Ramanujan’s writings: the objects described in his deathbed letter, which Ramanujan called “mock-theta functions.” Their purpose had been a mystery for a hundred years.
“Wanna see something cool?” Ken asked me one day. He took me into his office and sketched out a proof.
Some mathematical functions spit out numbers of such enormousness and in such a torrent that the apparatus of mathematics breaks down; the pile of numbers becomes a hill too steep to climb. Such functions are said to “blow up” to infinity. The purpose of the mock-theta functions, Ken realized, was to clear the path. Using the mock-theta functions, Ramanujan had found a way to carry himself over the infinitely steep hill, all the way to the gates of infinity itself, and then, miraculously, to disappear through a keyhole and come out on the other side. The path through was head-splittingly implausible, but Ken had shown me that it lay where Ramanujan had said it did.
Ken finished the proof just in time for Ramanujan’s birthday, and for inclusion in the lecture series being held all across India to mark it. We bought plane tickets. We had good news to share: in 1920, on a bed in Madras, as Ramanujan was contemplating his coming encounter with the infinite, he found a way through.
But I wondered, Could I find a way to imagine myself into some kind of conversation with Ramanujan, as I had with my other heroes when I was a kid in Ruston?
Maybe not. With Ramanujan, there was no book of studio photographs, no paper trail to insert me into his headspace. Paper had been too expensive to buy, so Ramanujan did almost all of his work on a small slate, writing down his highly compressed formulae onto a scrap of paper only after many hours of work, erasing the slate every few seconds. A typical page in one of his three “notebooks”—really just piles of scrap, bound after the fact—contains no words of explanation, just equations, symbols, and strings of digits. Only four photographs of Ramanujan exist, and two of them are nearly identical. He had no children. His family, including his widow, are all dead. There was nothing to grab onto. I would have to rely on other, less direct, ways of knowing.
2.
At Mysore, 12 degrees north of the equator, we boarded a sleeper car on the Mayiladuturai Express, a rusty train that would take us even farther south, to the two-thousand-year-old city of Kumbakonam. The city was only 250 miles away, but the trip would take fourteen hours.
The scenery along the tracks was bewildering in its contrasts, as though Eden were occupying the same space-time as a post-nuclear Florida. A goatherd in a vermilion loincloth squatted among smashed-in computer monitors and broken circuit boards—an image of Paleolithic man zapped forward to the end-time. A field of sugarcane and mango trees gave way to an industrial junkyard, where long-horned zebu moved among rusted machine-heaps, looking for garbage to eat.
I opened my notebook and started playing with a way to take Big O of the coefficients of divergent infinite series and create a metric space—a kind of nonsense, an attempt to measure immeasurable quantities, then arrange them in terms of how immeasurable they were. What would the genius do? Ramanujan might start by posing a crazy question that didn’t seem worth wasting a moment on, such as this one. Then he’d take a few angelic leaps of pure intuition and arrive at an unexpected new truth. I was like a cat trying to extricate itself from a five-dimensional paper bag.
The sight of me writing must have given Ken hope that my homework, now weeks late, might finally be done.
“Robert,” he called out, “let me see that notebook.”
I passed the notebook back to Wadim Zudilin, a Russian number theorist whose push-broom mustache and black-framed glasses made him look like he was always in disguise. Wadim passed it to Ken.
Ken scanned the page and frowned. This was obviously not homework.
Then he laughed, seeing how closely I was imitating the master. “Robert! You should be doing your homework! You can’t have dessert before dinner.”
As the sun set, it grew harder to fight off half a planet’s worth of jet lag, but I had homework to do, so I tried to stay awake. Wadim and I talked about music. When I told him that the last Apples record had been influenced by Electric Light Orchestra, he arched an eyebrow at a high Slavic angle and looked me solemnly in the eye.
“I love the Electric Light Orchestra,” he said. “I have all of their records.”
Soon everyone was asleep, stretched out on folding cots. The moment the car was dark, as though a bell had been rung, cockroaches flooded out to scour the floor and walls. I took my notebook to a semi-enclosed space between the train cars, in search of a light bulb to do my homework by. A metal gate, ajar and clanging in the wind, opened onto the countryside. A little dog trotted alongside the train, hopping over railroad ties and easily keeping pace.
All along the tracks lay burst bags of garbage. We were in the middle of nowhere. Where did all this trash come from? An answer appeared as the door opened and a flashy corporate type with a ring on his finger came outside, carrying a plastic bag full of garbage. He said something to me in Tamil, then crouched down and shoved the bag into the gap between the floor and the flimsy fabric wall, where it lodged. He stood up and pushed it through with the toe of his dress shoe. It was immediately shredded by the wheels of the train. Before returning inside, he bobbled his head and made a show of dusting off his hands: a job well done!
The train slowed as it approached Erode, Ramanujan’s mother’s ancestral home, where she had come to give birth. I hustled back into the dark sleeper car.
“Ken,” I whispered, “we’re stopping at Erode. We should get off the train!”
“We’ll only be stopped for, like, three minutes,” he murmured.
“But this is where Ramanujan was born,” I said. “This is awesome. We have to experience it.”
Dick Askey, a number theorist who graduated from Harvard in the 1950s, briefly woke up.
“It is not awesome,” he said. “It is merely good. You are softening the language. It is a bad habit, and you’ve got to break it.”
In the predawn darkness, a few commuters were out on the platform, reading the newspaper, nodding off on benches. We dawdled and took pictures. Through a hedge of flowers, I could see the lights of Erode.
To the left and the right, the train tracks vanished in the distance. Imagine the number line. In the middle is zero, the origin. To the right lie the positive numbers; to the left, the negative numbers. They go on forever in both directions, with an infinity at each end. Between them, as though between the terminals of a battery, the numbers leap into existence. As a boy, Ramanujan discovered that if he skipped along the number line, gathering and adding numbers according to simple patterns, when he arrived at infinity the sum could be a single, sensible number, like one or one hundred, or even π, a number with infinitely many digits that, like the avatars of the Infinite God, Vishnu, can never be fully written down. He discovered the series that yielded the basic trigonometric functions sine and cosine, and realized that the infinite series was the deeper definition not only of these but of all numbers. (In fact, Leonhard Euler had made the same discovery about sine and cosine in the eighteenth century. When Ramanujan found out that he’d been scooped by the great Euler, he was not elated, but ashamed—mortified, even, and hid his work in the roof of his house.)
The European mathematician who most famously grappled with the infinite, though in the rigid logic of nineteenth-century German science, was the brilliant, tragic Georg Cantor. Cantor saw infinity not as a blessing, but as a problem to be attacked and broken into pieces, the number line a road to be plotted and rigorously mapped. The number line was “a path which never breaks off.” It had to “remain passable wherever the journey may lead,” even as functions blew up and spat out impassable oceans of numbers. Cantor’s mania for mapping this flooded terrain led to greatness after death but disgrace in life.
Prior to Cantor, infinity was a streak of insanity in the Western collective consciousness. The pre-Homeric Greeks, Aristotle, and contemporary Europe had rejected mathematical infinity outright. Yet, paradoxically, Christianity required infinity, for God was infinite. And since He was infinite, Cantor argued, His mind must contain all numbers. In which case numbers were not only infinite but also completed—an endless array that nevertheless had an end, and could therefore be held in the mind as a single object, then classified and studied.
Over fifteen years, Cantor proposed a brain-breaking taxonomy of greater and lesser infinities. Cantor’s colleagues rejected his work as, at best, wrong-headed, but Cantor saw no conflict between Christianity and mathematics, nor much of a difference. “A more powerful energy,” he said, had communicated the theory to him; the theory had come to him from God, “the first infallible cause of all created things,” and it proved His existence. For the primary characters in his syllabary of the transfinite, Cantor used not x and y but the Greek letters alpha and omega, the biblical symbols for God’s infinite nature.
By considering the idea of infinity seriously instead of as an inert article of theology, Cantor found himself in a territory so flaky that he was accused of being a pantheist. It was maddening—Cantor intended his mathematics to be used to complete Christian theology, yet here he was being accused of paganism. The mathematical establishment abominated Cantor. His own doctoral adviser, the great, grumpy Leopold Kronecker, sabotaged Cantor’s career and called him a “corrupter of youth.” The identical charge had driven Socrates to suicide some thousands of years ago; Cantor would be in and out of nerve clinics for the rest of his life. He died in a sanatorium in 1918.
Askey appeared in the door of the train, fussing that it was about to start moving. Ken thought we might be able to race the train on foot.
No one dates back to the days of Ramanujan anymore, but Dick Askey comes close. He knew one of the mathematicians who worked with Ramanujan during his time at Cambridge, a “jovial, short, plump” number theorist named John Littlewood.
“We have no idea how Ramanujan did the marvelous things he did,” Askey says, though it had taken him a while to see the depths in Ramanujan’s seductive, flashy formulae. “I’d heard about him, of course, and somewhere along the line bought his collected papers. But I didn’t look at them seriously.”
At first, Askey had found Ramanujan’s math odd and opaque, too eccentric to be of much use. Anyway, it was unrelated to Askey’s main interest, a class of special functions called orthogonal polynomials. They were proving difficult to crack. His research was leading him further and further afield, into an abstruse new area of mathematics, called coding theory, that seemed related to orthogonal polynomials, though he couldn’t discern the point of connection. There was no one in Askey’s math department at the University of Wisconsin, Madison, with the right expertise, and so, in perplexity, Askey reached out to George Andrews, the hero-mathematician who had just discovered Ramanujan’s final “lost” notebook in a library, in the belongings of another professor, long dead.
The discovery of the lost notebook was the final miracle in the Ramanujan story. “I have a hundred-page, unknown manuscript of Ramanujan in my briefcase,” Andrews told Askey when he arrived in Madison. “You can have a look at it for a nickel.”
Soon, all became clear: Ramanujan had foreseen the problems Askey was facing. Reading from Ramanujan’s spell book, and with Andrews as the medium, Askey compelled the orthogonal polynomials to yield their secrets. But there was weirdness afoot, of a prototypically Ramanujanian variety.
“Ramanujan knew nothing about orthogonal polynomials,” Askey says. And he certainly knew nothing about coding theory, a subject that had come into being years after his death. Yet he seemed to have anticipated that these subjects would one day exist, that they would be interesting to someone, and that there would be problems associated with them that would need to be solved.
The simplest explanation is that Ramanujan was a time traveler from the future.
“It’s completely perplexing,” says Askey. “Since the orthogonal polynomials, I’ve spent much of my time working in Ramanujan’s garden.”
Around 1980, Askey read an interview in the Hindu magazine with Ramanujan’s widow, Janaki Ammal, that had gotten under his skin. When Ramanujan died, his jealous mother rejected Janaki, throwing her out of the house poor and unskilled. Janaki was still a girl, uneducated, and after her husband’s death she lived a hard life, even by the standards of southern India. By the time Askey read the interview, she was near the end of her life, half-blind and living on a pittance. The government had promised her at least a statue of her husband, whom they recognized as an Indian national hero, but they’d never delivered.
“Nothing matters now,” Janaki told the interviewer in the Hindu. “When I needed help, no one was around. Now it’s too late.”
“In this interview in the Hindu,” Askey says,“she lamented, ‘Where is the statue?’ I wasn’t smart enough to think immediately that something ought to be done. But within a few weeks, I realized that if we waited for the government to build a statue, Janaki would be dead before it happened. I thought we ought to give her something to show her how much the mathematics community cared.”
Askey commissioned a statue himself, and provided a sculptor with a second-generation photocopy of the only clear photograph of Ramanujan in existence. He could have quickly raised all the money he needed with a few phone calls. Instead, he sent letters to a hundred colleagues around the world, asking for twenty-five-dollar donations. He wanted Janaki to feel the weight of the love the mathematics world bore her and her husband.
Before Ramanujan left Kumbakonam, Janaki said, he’d been fat and cheerful. After five years in England, he was hollowed out by malnutrition and misery, perhaps carrying a parasite, perhaps infected with tuberculosis, and in a frighteningly deep depression. He’d heard nothing from his wife the entire time he’d been abroad; his mother had been intercepting Janaki’s letters and destroying them.
“If only you had come with me to England,” Ramanujan told Janaki, “perhaps I would not have fallen ill.”
There’s a theorem, Askey says, that states that no finite number of images can be used to reconstruct a three-dimensional object, such as a face, exactly. Nevertheless, when Askey delivered the bust to Janaki, depicting a chubby, youthful Ramanujan, “she said it was as if his spirit had returned. She garlanded it every day.”
Janaki was ninety years old by now, but wrote a letter of thanks to every mathematician who’d made a contribution.
Eleven busts were commissioned and sold to mathematical eminences around the world. One stands in George Andrews’s house. But mathematical megastardom is one of the more anonymous forms of celebrity, and a few years ago one of the busts ended up in an estate sale, in the custody of an auctioneer who knew nothing about Ramanujan. A mathematics professor bought it.
“It’s not where it belongs,” Askey says. “Ken should have it.”
3.
Ken Ono has spent most of his career working a particularly fertile patch of Ramanujan’s wild garden, discovering the subterranean connections and root systems that connect it to the forest of world mathematics.
“It’s not unusual for experts to totally miss the point of Ramanujan’s formulae,” Ono says. “That happens over and over again. Everyone has four or five favorite examples when they’ll say, ‘I thought I understood this formula. I wrote papers on it, only to discover, five years later, that I’d missed the point.’”
Ono, now forty-six and slender as a greyhound, was all but indifferent to mathematics when he was growing up in Baltimore. He was good at it, but he got good grades in everything without having to study or try very hard. (“I was that kind of kid,” he says. “You know the kind.”) His immigrant father, Takashi Ono, was a number theorist at Johns Hopkins who worked from home, so Ono saw the work of mathematics every day. It wasn’t appealing to him. The elder Ono didn’t seem to do much more than sit around the house, presumably thinking deep thoughts, and occasionally write something down. Like other Japanese men of his generation, Ken says, he rarely showed much emotion, and gave no outward signs of the exaltation that mathematics could bring. Math seemed to be just another dreary ritual of adult life, like polite conversation or public radio.
Ono was an athletic kid with ambition and talent, and raced bicycles on a national circuit. (For the past few years, he’s been a triathlete on Team USA, and trains continually, even while abroad on math junkets.) As a teenager, he was promising enough to earn sponsorships from Bianchi and Avocet. He was not interested in sitting still or thinking about numbers. His father was not interested in racing.
“He thought it was kind of silly,” Ono says. “He let me do it, but I always had to get people to pick me up and drive me. I think he watched me race only once.”
Ono dropped out of high school in the eleventh grade and spent his free time on his bike. One day in the spring, preoccupied with the National Capital Open, in Washington, DC, he rode back home from a long morning of training in the countryside, stopping at the mailbox to check for college acceptance letters. He pulled out a yellowed envelope, obviously foreign, that was addressed to his father. He wrangled his Trek inside and handed his father the letter.
At the sight of the return address, his father staggered to the couch. He read the short letter, typewritten on rice paper, in silence.
Dear Sir,
I understand from Mr. Richard Askey, Wisconsin, U. S. A., that you have contributed for the sculpture in memory of my late husband Mr. Srinivasa Ramanujan. I am happy over this event.
I thank you very much for your good gesture and wish you success in all your endeavours.
Yours faithfully,
S. Janaki Ammal
Ken’s father, normally so impassive, covered his face with his hand, seemed to crumple, and wept.
“That was the first time I heard the story of Ramanujan,” says Ono. “It made all the difference in my life.”
At the University of Chicago, Ono switched majors, from premed to math. He was drawn to Ramanujan’s whiz-bang formulae, but after giving them a once-over, it seemed to him, as it had to Askey, that they weren’t all that deep. They were just “crazy tricks that did something weird.”
Ono’s personal opinion was irrelevant. Ramanujan’s mathematics wasn’t widely taught anymore; no one outside of a few specialists studied him seriously. Though he’d had a brief vogue shortly after his death, and a resurgence in the 1960s, Ramanujan was unfashionable. His body of work consisted of notebooks filled with short formulae, so there was no overarching theory to study, and formula writing had been out of style in serious mathematics for more than a century.2 The formulists had had their time. They were the sorcerers of math’s prehistory who had discovered the deep connections among the key concepts and encoded them in mathematical haiku. Modern mathematicians-in-training studied modern theorists, technicians who labored over proofs of narrowly defined conjectures, mastered this or that technique, and polished the gleaming apparatus free of fingerprints.
When Ono began to dig a little more deeply into Ramanujan’s formulae, he was surprised at the tangle of roots he encountered below the surface. Ramanujan’s crazy tricks linked up with some of the deepest concepts in math. They could not exist unless they concealed massive theoretical edifices.
Take the tau function, an oddity that Ramanujan discovered and studied during his five years at Cambridge. A function is a mathematical expression that, when fed with a number, produces another number. It’s a machine that takes some raw material and then stretches, compresses, reshapes, or transforms it into something else. Functions embody the relationships between numbers; they are central objects of study in number theory. Ramanujan found the tau function important enough to spend upward of thirty pages in his notebook exploring it, but it was hard for other mathematicians to see why he’d been so interested. On its face, there was nothing special about the tau function. Hardy, Ramanujan’s chief collaborator at Cambridge, worried that the tau function’s homeliness might lead future mathematicians to see it as a mathematical “backwater.” For decades after Ramanujan’s death, it was treated as one.
Then, in the 1960s, a French mathematician named Jean-Pierre Serre realized that the tau function was an unassuming front for a powerful force. Its existence could be explained only if there was a brand-new theory of functions encoded in it. Serre called this theory, suspected but not proven, the Galois representations. Not long after, the Belgian researcher Pierre Deligne proved that the Galois representations actually existed, and in the process clarified that the tau function was deeply connected to algebraic geometry and algebraic number theory. For proving the Galois representations, Deligne won a Fields Medal, the ne plus ultra of mathematical achievement, awarded every four years to a mathematician under the age of forty. In 1995, the Galois representations appeared as the key component of Andrew Wiles’s epochal proof of Fermat’s Last Theorem, the largest, most notorious open problem in mathematics, which had gone unproved for over three hundred years and was suspected of being unprovable. Wiles, forty-one when he published the final version of his proof, was ineligible for a Fields, which only seems unjust: no prize, not even a Fields medal, could be adequate to the mastery in his proof. When the International Mathematical Union convened to hand out Fields Medals that year, it created a special award for Wiles and, for the ceremony, built two stages: one for the Fields Medalists and one above it, where Wiles stood alone.
“All that, from Serre to the Fields medal to Wiles, is from only about ten or fifteen pages from Ramanujan’s notebooks, out of the hundreds that he wrote,” Ono says. “Which is typical! And in fact, studying the tau function, the British mathematician Louis Mordell proved some properties that were later developed into Hecke algebras and the Langlands program, among the two or three most important developments in twentieth-century math. And that’s from a different five pages of Ramanujan’s work on tau that have no intersection with the previous fifteen. In fact, it might be as short as a page. One page from Ramanujan’s work may have given birth to all that.”
There’s a subtlety here that needs to be made explicit. It’s not remarkable that Ramanujan’s work on the tau function led to interesting new mathematics. That kind of thing happens all the time; it’s how the subject advances.
With Ramanujan there is a seeming reversal of cause and effect. No one can write down a formula with deep, hidden properties unless they first know what the deep properties are that they are trying to encode. This is the way mathematicians understand math to work; it is the only way they—we—know to approach the subject. But the significance of the tau function—the reason to write it down—wasn’t discovered until Ramanujan had been dead for sixty years.
“There’s no way Ramanujan knew all these intermediate things,” says Ono. “The concepts [encoded in the tau function] didn’t exist when he was alive. That’s the mind-boggling part: Ramanujan anticipated the work of people who would live long after him. He had visions that said there were going to be some theories in the future. Somehow. He didn’t need any intermediate steps for him to anticipate that there would be all these subjects, and that he would find the first examples of them, and that they would go on to be the prototypes that we desperately needed to build our subjects. Whether he’s in fashion or out of fashion has more to do with us, with where we are in coming to grips with him.”
When Ono started looking into the mock-theta functions, there were a few hints as to what they might mean. They seemed to help describe the spread of cancer tumors, and physicists had begun to find them useful in understanding how black holes unravel space and time and how string theory knits them together. This was peculiar, since the concept of string theory didn’t exist in 1920, when Ramanujan wrote his letter, and black holes were brand-new objects of speculation among a handful of physicists. But still—when modern astrophysicists peer inside their black-hole models, they find they are looking at mock-theta functions.
Despite a few research applications, the mathematical understanding of mock-theta functions was in a bizarre state. Dozens of papers had been written on them, but no one could explain in the most basic sense what a mock-theta function was. When Ramanujan died, there were no clues anywhere in the mathematical literature to explain why he found the mock-theta functions interesting. It’s probably not going too far to say that, in fact, they weren’t interesting. All they did, Ramanujan wrote, was imitate a class of functions called the theta functions, which had been around for a century or so. In that time, the theta functions had been working perfectly on their own. No one had needed to imitate them. Ramanujan had produced a solution to a nonexistent problem. Who cares? would not have been an unreasonable response.
In the summer of 2012, Ono found that the only way he could understand the mock-theta functions was via Serre, Deligne, and others’ work on the tau function. This made no sense. It meant that it was not Ramanujan’s own work on tau that had led Ramanujan from tau to the mock thetas, but the work of others, of Serre and Deligne, that would not be carried out until he’d been dead for decades.
Ono had the sensation of Ramanujan walking in his footsteps, but from the wrong direction in time.
“Whatever Ramanujan was thinking about between the tau function and the deathbed letter somehow must have been parallel to what I was doing, without him knowing I was doing it, ninety years later,” he says.
With Ramanujan looking over his shoulder like a “chubby guardian angel,” Ono found that, as the numbers being spit out by the theta functions started to grow at an unimaginable speed, approaching and then far exceeding the number of atoms in the universe, the mock-theta functions began to imitate them with eerie precision. In the lower reaches of the number line, the behavior of the function and its doppelgänger was unlovely and chaotic. But out here, in the immense realms that had driven Cantor insane and enraged the European mathematics establishment, their relationship became clear. You could take the ludicrous, unmanageable output of a theta function, then subtract the ludicrous, unmanageable output of a mock-theta function, and the answer was shocking in its simplicity. The answer was 4.
With pencil and paper and pages of calculations in front of you, to see these titanic quantities consume each other so precisely bends the mind.
“It doesn’t take any imagination,” says Ono, “to recognize that four is a beautiful number.”
As Ramanujan lies dying, racing toward infinity, a dot of light appears in the great wall. The gleaming apparatus is about to crash, but the mock theta function does its crazy trick, and the infinite dissolves, just a little. A portal the size of an atom appears. The apparatus threads the hole. And then it keeps going, and going, and going…
4.
The train pulled into Kumbakonam station at six in the morning. The sun glowed just below the horizon. The air was dark and moist and hot, like the inside of a monster’s mouth. The antimalaria drug I was taking was starting to go a little psychedelic on me, casting a greasy iridescence over my qualia. Mosquitoes whined in my ears like winged synthesizers. Up and down the platform, the bodies of sleeping commuters with overnight connections lay on woven mats, occupying every horizontal surface available, like felled stalks of wheat. I was nauseated and precarious, as though with a belly full of stomach acid and psilocybin.
From the other side of the platform, a deputation of professors from SASTRA University (the Shanmugha Arts, Science, Technology and Research Academy) shouted over to Ken and started making their way over, waving copies of the Hindu. Ken’s glorious work on the mock-theta functions, they said, was being praised in all the papers. They led us outside, toward a bus waiting to take us to our bungalow, in a little villa just outside of town. In the street, a group of schoolboys in matching polo shirts and shorts caught sight of Ken and started whispering to one another, stealing glances at him as we walked by. One of them stepped away from the group and pointed straight at the famous mathematician.
“Jackie Chan,” he said. “Jackie Chan!”
The rest of the boys joined in, yelling, “Jackie Chan!” as they rushed over and mobbed Ken. “Jack-ie Chan! Jack-ie Chan! Jack-ie Chan!”
Ken patted them on their heads, saying, “Hello, hello, how are you? So nice to see you,” and so forth, then posed for a picture, holding his hands jauntily out to the side, in the hang-ten surfer mudra.
“This happens every time I come here,” Ken said.
From inside the van, Kumbakonam manifested as a blur of low buildings along a dusty, curbless street. Piled up higgledy-piggledy were the huts of the poor, the ragged condos of the upper-middle class, and chaoses of splintered wood, dirt, and junk. Relics from antiquity seized the eye. A stocky stone avatar of the Infinite God, standing with the nonchalance of a fire hydrant, was surrounded by a spillage of brick and shredded roof-thatching from a house that had collapsed into the street. Behind a wall made of fresh brick, tarp, and rusted metal barrels rose a temple’s entrance-tower, the gopuram, minutely carved and painted in all the pastels of the Indian palette, erected centuries ago. Somewhere back there, in the interior of the two-thousand-year-old city, was the temple itself.
The khaki exterior of SASTRA University was smooth and modern. SASTRA opened in 1984, and acts as a conservator of Ramanujan’s legacy. Though Ramanujan flunked out of college twice—spectacularly, earning grades as low as 10 percent in some subjects—he dazzled his math instructors, who couldn’t tell if he was a charming genius or a holy lunatic. They tried to help him, but how could they? They didn’t understand the first thing about him.
As Ramanujan entered adulthood, he was a soul going to waste. Unless he could get out of Kumbakonam, he would be subsumed by it, his discoveries lost forever. But when Hardy’s emissary appeared in Kumbakonam, offering Ramanujan a position at Cambridge, Ramanujan said he couldn’t go. The Infinite God had appeared in a dream, telling him that the time had not yet come for him to share his gift with the world.
In any case, foreign travel was impossible. Kumbakonam was a place where culture and religion were completely intertwined. Ramanujan was a Brahmin, the caste of priests and intellectuals; a Vaishnavite, who regarded Vishnu as god over all and who worshiped his local avatar, Narasimha; and an Iyengar who kept to a complex diet that prohibited all meat, but also cheese, onions, salt, rice on some days, food of any kind on others, and governed who was allowed to prepare his food, and in what state of ceremonial purity, and with whom he was allowed to eat. To live abroad would be to abandon this web of identity. It would be an act of self-destruction, a form of suicide, really.
Hardy’s emissary persisted. Ramanujan went to Namakkal, a nearby temple-town, and slept on the temple grounds for three days, until the goddess, Namagiri, avatar of Lakshmi and wife of Narasimha, appeared, granting him permission to leave.
While he was in England, Ramanujan woke up in the morning and did puja, prepared his food in a state of ritual purity, painted the namam on his forehead and then erased it—but on the day he sailed for England, he wept as he cut his kutumi, a braid that would have set him apart as an alien. If he left, he told his English escort, it would break the web that bound him to the world, and it would never hold him again. His place would be destroyed forever. If he ever returned, he would no longer make sense as a being. To the people around him, he would not exist. He would haunt his own life as a ghost, ignored. But Namagiri had given him permission, so he left.
During Ken’s lecture on the mock-theta functions, an Indian professor collapsed in the heat. “Stay with me, Krishna!” his wife cried.
The effects of the antimalaria pill crept back up on me. I felt suddenly ill and hurried to the bathroom to splash water on my face. Through the open window drifted all the smells of Kumbakonam: clouds of roasting spices and fresh fruits mingled with manure and rotting garbage and the reek of the Cauvery River. In one of the stalls, a Western mathematician was on his knees, vomiting. “The smells are just too strong,” he said, “much too strong.”
Outside, the streets were a pandemonium. It was at least 100 degrees. An icy prickle raced back and forth across my scalp. My head swam and my ears rang. A high-low honking was getting close, quickly, but I didn’t see the car until a chrome fender stopped an inch from my kneecap. The driver’s face behind the glass was expressionless. A thought appeared in my head, in words: This is not safe.
Then I was in the narrow jumble of Sarangapani Street. Ramanujan’s small house, preserved as a museum, stood next to a hardware store. Its door and single window were painted powder blue. Four blue posts held up a low roof, thatched with palm leaves in Ramanujan’s time, now covered in red tiles. When it grew too hot inside, especially during the summer, Ramanujan would bring his slate out here to lie on a cot, sometimes all night and into the next day, to do his research. To preserve his bubble of concentration, his mother quietly pressed curd rice into his hand while he worked.
A hallway led from the front door to a second, inner door. Beyond it was a small common room the width of a hallway, a galley kitchen, and a shrine for doing puja. It was dark inside the house, with a little light coming in through the murra, an interior courtyard that was open to the sky and the rain. I sat on Ramanujan’s bed. I was as close to him as I would ever be. A slate, similar to the one he had used, lay across it—scene dressing provided by SASTRA. I held it on my lap and closed my eyes, rising and falling on waves of nausea.
All mathematicians—the great, the good, and the average—have a mentor and arise via a pedigree. Hecke was taught by Hilbert, Hilbert by von Lindemann, von Lindemann by Klein. Cantor was taught by his future antagonist, Kronecker (and by Frobenius and Weierstrass), Kronecker by Dirichlet, Dirichlet by Poisson (and Fourier). Noether had Gordan, Gordan had Jacobi. Dedekind, Riemann, and Möbius all studied under Gauss. Fourier had Lagrange, Lagrange had Euler, Euler had Bernoulli fils, Bernoulli fils had Bernoulli père. The chain is how the discipline is communicated down the centuries, stored in the collective mind of a culture rather than in individual minds, which are too small to contain it.
Ramanujan had had an out-of-date elementary math textbook and whatever was in the air. For five years after he flunked out of college, this room was where he worked, looking out his window, becoming who he became. How did he do it?
A sign in Tamil and English hung on the wall: Ramanujan used to sit here for hours looking through the window. Southern India is an ancient and unchanging place. The Kumbakonam of today is the Kumbakonam of a hundred years ago, despite trinkets like cell phones and automobiles. Walk out Ramanujan’s front door and you see what he saw. You see through his eyes.
What was the genius trying to tell me?
I walked out his front door. Virtually next door, the gopuram of Sarangapani Temple rose into the sky, a massive and intricate piling-up of what seemed like the entire Hindu cosmos in a pyramid of entwined limbs, naked bodies, animals, celestial entities, and the Infinite God in his infinite incarnations. The infinity of creation, in a sacred, teeming heap, was the first thing Ramanujan saw when he stepped outside. It cast the neighborhood in shadow.
5.
The gopuram was the only part of the temple visible from the outside. The rest was concealed, an organ within the body of the city.
Taking off my shoes and passing through the gate, I left Kumbakonam and entered the city-within-the-city, an orthogonal space, larger on the inside than it appeared from the outside, that rambled down long corridors, ran up and down flights of stairs, opened onto stone-floored piazzas, and sprouted fractal sub-temples within itself. Carnatic music came from distant reaches of the city-within, in loud blasts and soft, continual trickles. Old men in little more than rags, retired from the city-without and seeking enlightenment, walked and chanted, collecting coins from passersby, while young parents, strolling through the city-within after dinner in the city-without, hustled around, chasing down screaming children, in a state of mind that was far from holy. It was a sacred place and a mundane one, which would be a paradox, except that Hinduism is so vast, it doesn’t recognize paradoxes. In Ramanujan’s time, and even now, there was no boundary between the spiritual and the material. The infinite dwelled in the temple and flowed out into the city. You received visions of the Infinite God; you saw your auntie in the street.
I followed the music. It led me to the shrine at the heart of the temple, a stone chariot drawn by elephants. A sound of ringing bells and droning voices began to grow. A loose band of worshipers turned a corner and approached. One of them gestured toward a staircase that led into another interior space. I climbed the stairs and, inside the sub-temple, came face-to-face with an old man who touched my forehead with a silver bowl and pushed a bouquet of flowers into my hands.
I sat on the stone floor and closed my eyes. The antimalarial delirium was fading again, leaving behind a drowsy calm. Phosphenes pulsed on the insides of my eyelids.
We’re told that Ramanujan was here at the temple almost as much as he was at home, doing mathematics and holding forth on his own private religion, an idiosyncrasy of Vaishnavism, which is itself an idiosyncrasy of the vast literature and culture that has come to be called Hinduism. He preached to the adults. He interpreted dreams. He recited Hindu scriptures, whose cosmologies contained enormous, unchristian numbers: no six thousand years of creation, but a history unfolding in cycles of time numbering in the millions and billions of years. No twelve tribes of Israel, but heroes like Rama, who commanded armies of 100,001,000,010, 000,000,100,010,000,010,001,000,001, 000,100,000,100,010,000,000,005 men. No One God above the angels and humanity, but Vishnu the sustainer, who embodied everything, including its opposite, including nothing. He was physically present in every atom of creation, yet entirely outside it. His body was the universe, yet the universe could not contain him. He was an immaterial being who resided in the Milky Way. He was a turtle, a fish, a boar, a dwarf, and the half-lion, half-man Narasimha.
Eight hundred years ago, the South Indian mathematician Bhaskaracharya wrote that dividing by zero yielded a number “as infinite as the God Vishnu,” a mathematical sacrilege that would have sent poor Cantor back to the laughing academy. Here in the temple, Ramanujan had spoken of something similar. The act of multiplying zero by infinity, he said when he was young, yielded all numbers simultaneously—the body of Ishvara, or God in its totality. Each number was a single act of creation among the infinitude that created and sustained the universe from moment to moment. Whenever there is injustice, says the literature, Vishnu enters the world as Krishna, Rama, Balarama, Parashurama, Narasimha. His forms are innumerable; they exhaust numbers. He was not infinite in size, like the indivisible YHWH of Cantor’s religion, but of infinite forms. His infinity signaled not madness but life and its continuous, momentary re-creation.
“My Lord, you easily assume any form you desire,” his worshipers chanted. “Your body includes all the worlds.”
I fell asleep leaning against the temple wall. I dreamed I was back on the train, traveling along the mock-theta function as it gathered speed in the far reaches of the number line. Somewhere else in time, Ramanujan was dying. Dick Askey sat across from me. His soft eyes were turned toward the night. The yellow lights of empty platforms strobed past.
Askey gestured outside.
“They are the singularities,” he said, the points where the mock-theta function shot off into infinity.
The train picked up speed, pressing me against the cabin wall. Straining against inertia, I turned to the window. The singularities streamed by as a river of light.
The train stopped.
“This is the nth root of unity. We are near Ramanujan’s home.”
I opened my eyes.
In the heart of the temple are the arcāvatāra, special avatars of the Infinite God made of stone and metal. For festivals and ceremonies, worshipers hoist one of them, the utsava murti, and carry it through the temple grounds. The murti is fully God. It becomes the infinite in its totality.
Cantor had said that we must understand mathematical infinity the same way we understand the infinity of YHWH. But YHWH’s qualities could not be known. “You cannot see my face,” the Almighty told Moses on Mount Sinai. “No one may see me and live.” The paradox ruined Cantor’s mind. The infinite was an alias for death.
But the infinity that Ramanujan knew was just a stone. His friends carried it past him as he sat here, his back against the wall and a slate across his lap. Ramanujan could see the infinite with his eyes open.
What is the idol trying to tell me?
That to watch the Infinite God approach was not a catastrophic death trip but a drawing near to a place of comfort. That even as he approached the infinite, Ramanujan found a wormhole through, and beyond. Even on his deathbed, mathematics was an act of worship. Worship of a single infinity, in infinite forms, all of them knowable.
The authors wish to thank Vasudha Narayanan, of the University of Florida, for her many impromptu lectures on the subject of Hinduism in South India.
- The golden ratio is also known as phi (ϕ), and is equal to 1.618034… Phi possesses a host of surprising qualities, but it can be generated simply, by drawing a series of squares. ↩
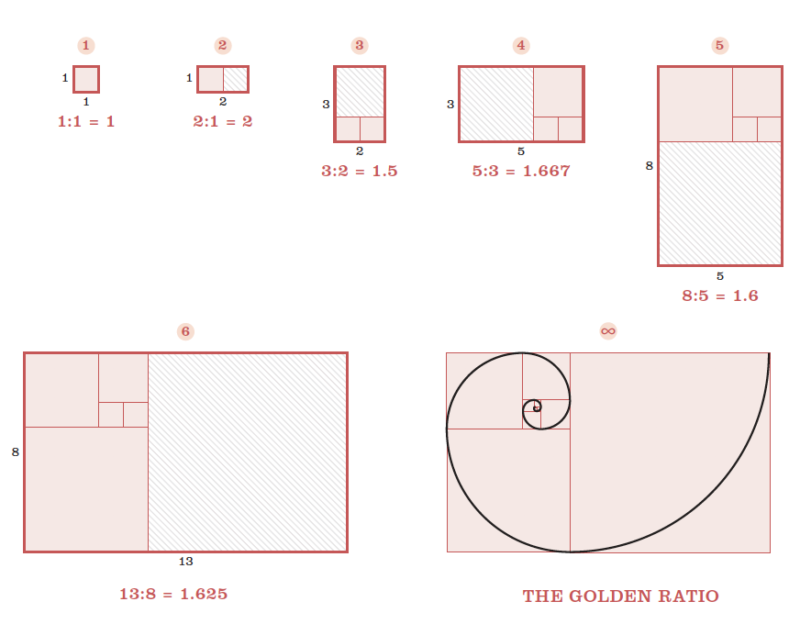
Building Phi
ϕ = 1.61803398874989484820458634365638117720…
The irrational number phi (ϕ), which has a host of strange properties, has long been an object of fascination for number theorists. Visual artists since the time of the ancient Greeks have found its graphical representation so pleasing that it has become known as the Golden Ratio. The digits of phi go on forever, and can be generated by mathematical expressions as intricate as you like. A classical expression uses only the number 1 in an eternally descending continued fraction. But you can also generate ϕ simply, by drawing a series of squares, then measuring the resulting rectangles and comparing the lengths of their sides. As you draw more squares, the ratio draws closer to ϕ, circling it in a tightening spiral: 1, 2, 1.5, 1.667, 1.6, 1.625… until, at the ∞th rectangle, you get ϕ exactly.

- A similar shift occurred in the English departments of the 1990s. One no longer roamed the inside of a poem to discover where its lines of influence lay, but studied the lingo-heavy theory that exposed the poor poet’s limitations. ↩





